难啊

一些基本概念

信号可以表示为时间的一个函数或序列，该函数图像就被称为信号的波形
一些信号的特性可能不能用函数来描述，但是可以有具体波形
信号分为以下的种类：

连续信号和离散信号

连续时间信号是在连续时间范围内有定义的信号，这里的连续指的是定义域的连续（所以连续信号可以含有不连续点），值域可以是连续的也可以是非连续的。
离散信号是仅在一些离散的瞬间才有定义的信号（离散信号无连续定义域）。
这本书新学的一个重点的时间信号是：$\epsilon (k)= \begin{cases} 0,k<0 \\\\ 1,k\geq 0\end{cases}$ ,他的名字为单位阶跃函数，其值域只有0，1两个数值。
目前定义有三种，主要区分点在于自变量为0时函数值不相同（一种是0点没有定义，一种是0点为1/2，一种就是我书写的这种，0点为1，我使用的教材为吴大正的信号与系统第五版，这是这本书上的定义。）
单位阶跃函数的导数为冲击函数：$\delta (t)= \begin{cases} \int^{\infty}_{-\infty}\delta (t)dt=1 \\\\ \delta (t)=0,t\neq 0 \end{cases}$
冲击函数只在0点有非0值并趋近于正无穷。（可以想象一个限定面积为1的矩形信号以y轴为对称轴，不断将其拉高使得其高度趋近于正无穷宽度趋近于0）

周期信号和非周期信号

周期信号是定义在$(-\infty ,\infty)$区间，每隔一定时间T或整数N（离散信号），按相同规律重复变化的信号。
不具有周期性的信号被称为非周期信号（T或者N趋近于无穷）

能量信号与功率信号

若信号f(t)的能量有界，则称其为能量有限信号，简称为能量信号。弱信号f(t)的功率有界，则称其为功率有限信号，简称为功率信号。仅在有限时间区间不为零的信号为能量信号，因为这些信号的平均功率为0，因此只能从能量的角度去考察，直流信号，周期信号阶跃信号这些都是功率信号，他们的能量为无限，只能从功率的角度去考察。一个信号不可能既是能量信号又是功率信号
对于连续信号是积分，离散信号是求和。

关于冲激函数的重要性质

冲激信号的广义函数定义：$\int^{\infty}_{-\infty}\delta(t)\varphi(t)dt=\varphi(0)$
由此可得: $\int^{\infty}_{-\infty}\delta(t-t_0)\varphi(t)dt=\varphi(t_0)$
由这两个式子可以推出冲激函数的取样性： $\int^{t_2}_{t_1} f(t)\delta(t-t_0)dt= \begin{cases} f(t_0),t_0\in [t_1,t_2] \\\\ 0,t_0 \notin [t_1,t_2]\end{cases}$
单位冲击函数为偶函数，
单位冲激信号的尺度变化:$在a\neq 0 时,\delta(at)=\frac{1}{|a|}\delta(t),\delta(at-t_0)=\frac{1}{|a|}\delta(t-\frac{t_0}{a}),\int^{\infty}_{-\infty}\delta(at-t_0)f(t)dt=\frac{1}{|a|}f(\frac{t_0}{a})$
单位冲激信号与普通函数相乘:$f(t)\delta(t)=f(0)\delta(t),f(t)\delta(t-t_0)=f(0)\delta(t-t_0)$
单位冲激信号的导数称作为冲击偶信号，冲击偶信号为奇函数。
冲击偶信号与普通信号相乘：$f(t)\delta'(t)=f(0)\delta'(t)-f'(0)\delta(t),f(t)\delta'(t-t_0)=f(0)\delta'(t-t_0)-f'(0)\delta(t-t_0)$
冲击偶信号的尺度变换特性：$在a\neq 0 时,\delta'(at)=\frac{1}{a|a|}\delta'(t)$

关于系统

信号的产生、传输和处理需要一定的物理装置，这样的物理装置常称为系统。一般而言，系统(System)是指若干相互关联的事物组合而成具有特定功能的整体。系统的基本作用是对信号进行传输和处理.
系统分类有很多，在此一一说明：

连续系统，离散系统，混合系统

连续(时间)系统：系统的激励和响应均为连续信号。
离散(时间)系统：系统的激励和响应均为离散信号。
混合系统(Hybrid Systems):系统的激励和响应一个是连续信号，一个为离散信号。如A/D，D/A变换器。

动态系统与即时系统

动态系统也称为记忆系统，若系统在任一时刻的响应不仅与该时刻的激励有关，而且与它过去的历史状况有关，则称为动态系统 (Dynamic system)或记忆系统。否则称即时系统(Memoryless system)。

单输入单输出系统与多输入多输出系统

单输入单输出(SISO/single input single output)系统：系统的输入、输出信号都只有一个。
多输入多输出(MIMO/multi-input multi-output)系统：系统的输入、输出信号有多个。
注意：多个输入输出指的并不是多维输入输出的情况。

线性系统与非线性系统

线性系统：指满足线性性质（齐次性和可加性）的系统。
齐次性：f(·) →y(·) 可推出 af(·) →ay(·)
可加性：f1(·) →y1(·)，f2(·) →y2(·) 可推出 f1(·) +f2(·) →y1(·)+y2(·)
*所以线性性质可以这么写：af1(·) +bf2(·) →ay1(·)+by2(·)
动态系统是线性系统的条件：动态系统不仅与激励有关，也与系统的初始状态有关，初始状态也可以叫做“内部激励”。满足动态系统输出可分为零输入响应的输出以及零状态响应的和（可分解性），以及零输入响应与零状态响应均为线性时为线性系统。
反之则是非线性系统

因果系统与非因果系统

因果系统：指零状态响应不会出现在激励之前的系统。
比较迷的玩意，一半都是因果的。一般是没什么东西是在激励之前就出响应的。

时不变系统与时变系统

时不变系统：指满足时不变性质($f(t)\to y_{zs}(t)\Rightarrow f(t-t_0)\to y_{zs}(t-t_0)$)的系统。时变系统反之。

这门课程主要学习LTI系统，即线性时不变系统。

LTI系统分析

LTI连续系统的时域分析，主要是建立并求解线性微分方程，这种方法也可以称为时域分析法。比较直观，物理概念清楚，是学习各种变换域分析法的基础。

用微分方程来分析LTI系统

我们可以把一个线性系统转化为微分方程的形式，方式如下：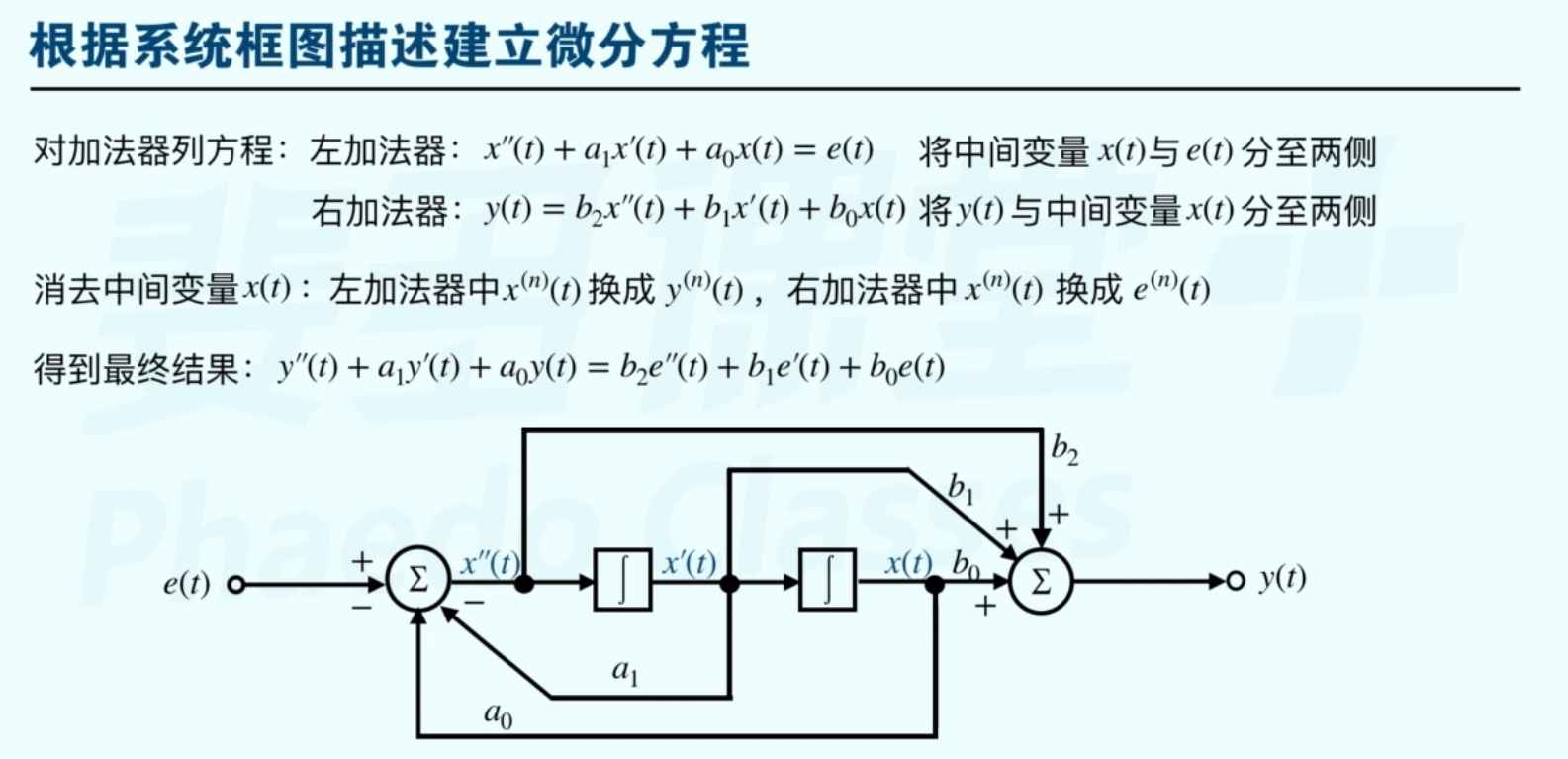

关于解微分方程的具体方法就很老生常谈了。

初始状态：$y(0-),y'(0-)...,y^{(n-1)}(0-)$反映历史信息，与激励⽆关，⼀般为已知。
初始条件：$y(0+),y'(0+)...,y^{(n-1)}(0+)$ 由初始状态和外加激励共同决定。
因为激励的加⼊，从$y^{(j)}(0-) 过渡⾄ y^{(j)}(0+)$时可能会产⽣跳变，即初始条件=初始状态+跳变量。
可以用冲击平衡法从初始状态来求初始条件：根据⽅程两边所含有的冲激函数及其各阶导数相同来判断是否跳变。

也可以分别求零输入响应以及零状态响应的方法来求得

冲激响应与阶跃响应

激励$e(t)=\delta(t)$时， 系统的零状态响应称为单位冲激响应，简称冲激响应，常⽤“$h(t)$”表
示。冲激响应$h(t)$反映系统特性，是后续分析涉及到的重要概念之⼀。 $e(t)=\delta(t)$ 时⽅程右端为 及其各阶导数的线性组合，$t>0$时⽅程右端恒为零，故冲激响应的形式与⻬次解的形式相同。

阶跃响应顾名思义就和冲击响应差不多，就是激励项变为了阶跃函数。求法和冲激响应的差不多，并且由于冲击函数通过积分可以得到阶跃函数以及LTI为线性时不变的，所以阶跃响应也可以通过冲激响应积分得到。

卷积计算

定义两个函数 $f_1(t),f_2(t)$ 的卷积为 $f_1(t)*f_2(t)=\int^{\infty}_{-\infty}f_1(\tau)f_2(t-\tau)d\tau$,其中 $\tau$ 为虚设的积分变量，积分结果仍为t的时间信号。
运算时通过被卷积信号的类型确定积分上下限，从而简化积分运算。
也可以图解法求解：

步骤⼀： $f_1(t)$与 $f_2(t)$变量置换，t变为 $\tau$，并将 $f_2(\tau)$以纵坐标为轴反折后的 $f_2(-\tau)$与 $f_1(\tau)$画在同⼀个坐标图中（横坐标为 $\tau$轴）。
步骤⼆：给定⼀个$t$值，将 $f_2(-\tau)$的波形沿 $\tau$轴平移，平移量为$|t|$，平移后的信号为 $f_2(t-\tau)$ , $t>0$ 时 $f_2(-\tau)$向右平移， $t\le 0$时$f_2(-\tau)$向左平移。
步骤三：将 $f_1(\tau)$与 $f_2(t-\tau)$相乘的到卷积积分的被积函数 $f_1(\tau)f_2(t-\tau)$。
步骤四：若 $f_1(\tau)$波形与 $f_2(t-\tau)$波形有重叠，则两信号的卷积积分为 $f_1(\tau)f_2(t-\tau)$在重叠区间的积分，若两信号的波形⽆重叠部分，则 $f_1(\tau)f_2(t-\tau)=0$，卷积也为零。
步骤五：令变量 $t$在 $( -\infty,\infty )$内变化，重复步骤2,3,4，最终得到卷积信号$f_1(t)*f_2(t)$。

卷积积分的运算性质：
顺便再说一下用matlab里的conv函数来做两函数卷积图像的代码：

t=-3:0.001:3;
t1 = -3 :0.0005:3;
y1 = stepfun(t,0);
y2 = stepfun(t,-1) - stepfun(t,1);
y3 = t1.* stepfun(t1,0);
y = conv(y1,y1);
l1 = length(y1);   
l2 = length(y2);  
l = length(y);
fprintf('%d',l);
subplot(4,1,1);
plot(t, y1);
subplot(4,1,2);
plot(t, y1);
subplot(4,1,3);
plot(t1, y);
subplot(4,1,4);
plot(t1, y3);

这样子写法会产生一个问题就是，在函数边缘区域的卷积结果会由于定义域的问题产生不对的结果，如图所示：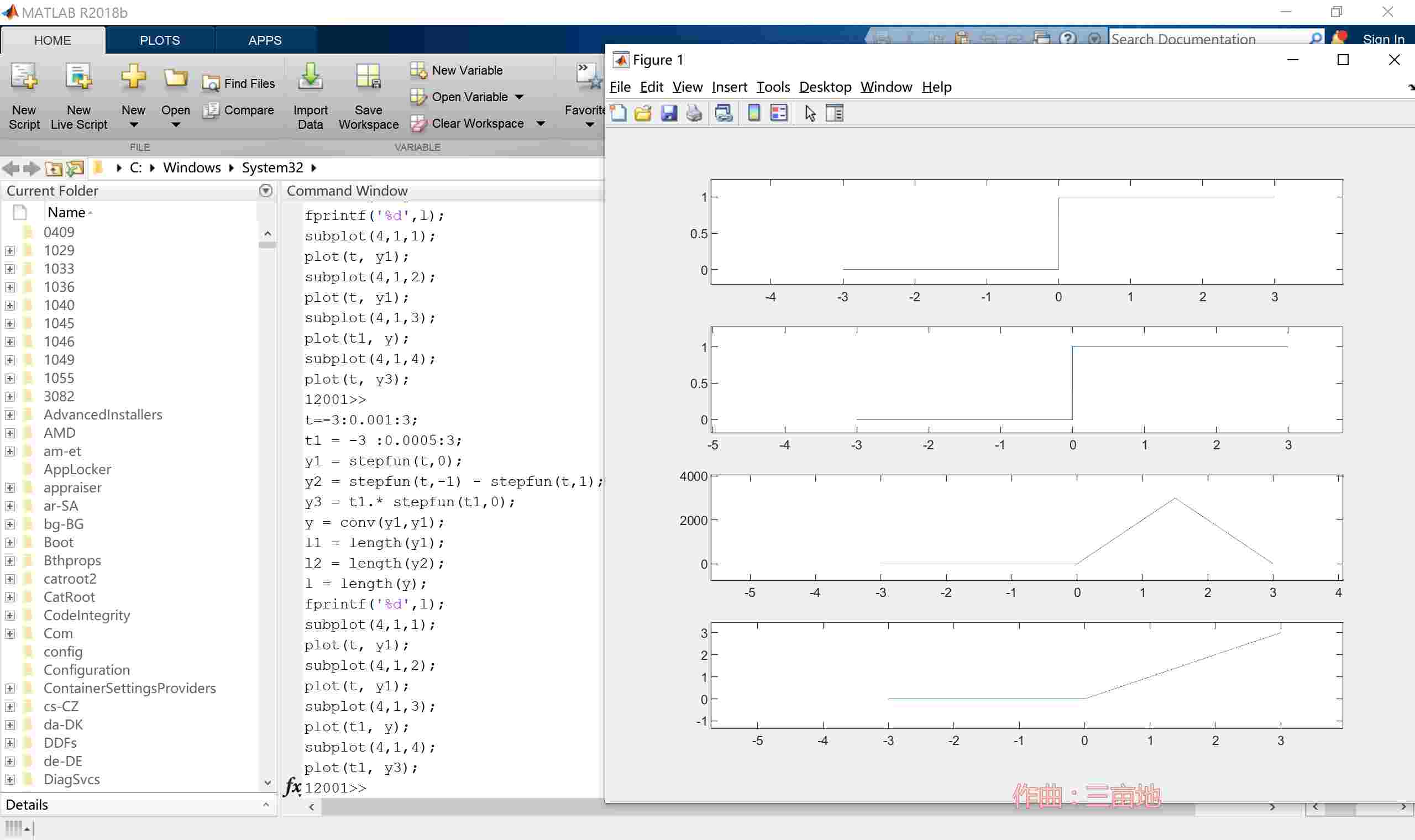

可以看出，图像只在定义域一半的区间是符合实际的，这点注意。

傅里叶变换

傅里叶变换是一种将信号从时域变为频域的方法，频域里函数有一些优于时域函数的性质，用频域来解析函数可以揭示了信号内在的频率特性以及信号时间特性与其频率特性之间的密切关系，从而导出了信号的频谱带宽以及滤波、调制等重要概念

正交函数集

学习傅里叶变换，首先要学习正交函数集的概念。
函数正交的定义是：定义在$(t_1，t_2)$区间的 $\phi 1(t)$ 和 $\phi 2(t)$ 满足 $\int_{t_1}^{t_2} \phi 1(t) * \phi 2(t) = 0$,则称这两个函数在$(t_1，t_2)$区间内正交。
正交函数集：若n个函数 $\phi_1(t) \phi_2(t) ... \phi_n(t)$构成的函数集中，两两在$(t_1，t_2)$区间之间相互均为正交函数，则称此函数集在$(t_1，t_2)$区间为正交函数集。
完备正交函数集：若在一个正交函数集之外不存在一个函数 $\delta(t)$ 使得 $\int_{t_1}^{t_2} \phi_i(t) * \delta(t) = 0$,呢么这个函数集就是完备正交函数集。

用线性代数的基理论来类比很容易理解这些概念，正交的函数就是两个不同的基，正交函数集就是很多不同的基组成的集合，完备正交函数基就是在当前空间里所有的基组成的集合。在线性代数里基组成了多维的向量，而在傅里叶变换中，我们需要用一个完备正交函数集来组成原函数（将原函数分解为不同集的组合）。
正弦函数集 $sin(n \Omega t),n=1.2.3...$就是一个完备正交函数集。也就是说我们可以用不同频率的正弦函数通过线性加减得到任意（连续可微）函数。
插一嘴，有时候可以看到使用cos函数也喊正弦，这么说是可以的，因为在频域中只要是频率相同这两个都能看作同一个变量，只不过是相位的差别。
（延申思考一下，一个相位）
这也是我们将函数从时域转到频域的方法————正弦函数集两个函数之间的不同只有频率上的不同，不同频率的正弦函数就可以代表原函数在这个频率上的分量。

傅里叶级数

简单的描述起来就是：傅里叶级数是函数经过傅里叶变换之后正弦函数集的幅值大小。
设原函数为$f(t)$，傅里叶级数$F_n$，呢么可以得到：$f(t)=\Sigma_{n=-\infty}^{\infty}F_n e^{jn\Omega t}$，其中$e^{jn\Omega t}$就是代表的频率,这是信号频谱的指数表示方法.
同时也有三角表示方法，即$f(t)=\frac{a_0}{2}+\Sigma_{n=1}^{\infty}a_n cos(n\Omega t) +\Sigma_{n=1}^{\infty}b_n sin(n\Omega t)$.或者也可以写成：$f(t)=\frac{A_0}{2}+\Sigma_{n=1}^{\infty}A_n cos(n\Omega t +\phi_n)$.

关于相位的问题，其实对于相同频率的正弦波信号，最终的相位是唯一的。因为频率相同相位不同的正弦波的叠加无论叠加多少都不会改变它的频率，最终频率的相位可以由$a_n,b_n$计算得到：$\phi_n=-arctan(\frac{b_n}{a_n})$.

周期函数展开为傅里叶级数：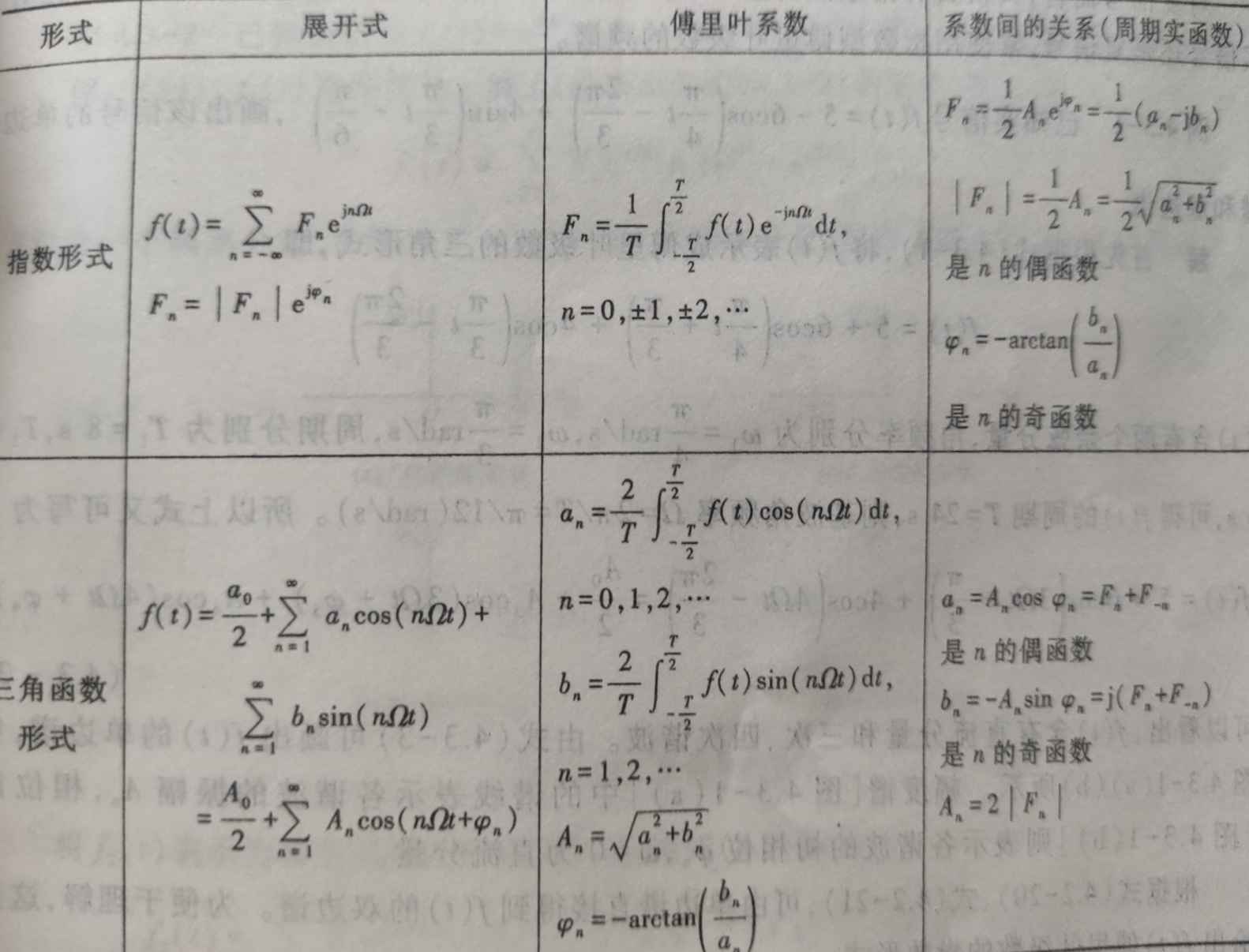

图片里面直接有傅里叶变换计算的过程，就直接把对傅里叶变换的理解说一下。从图片来看计算傅里叶级数的过程需要乘上$e^{-jn\Omega t}$然后再积分，这个也可以用基理论来解释，想象一个高维向量,$(x,y,z...)$,假如我们想得知这个向量在x这个基上的幅度，呢我们可以将这个向量直接乘上$(1,0,0,0...)$得到的数值就是x基的幅值。虽然不能直接比较，但是道理可以相通，傅里叶变换中的$e^{-jn\Omega t}$起到的就是$(1,0,0,0...)$这个向量的作用：筛选出对应频率函数所对应的幅值并且把其他的基的影响变为0（用到了正交函数的性质）。个人理解的大致就是这样。

周期信号的频谱

频谱包括幅度谱以及相位谱，由上面可以知道，一个固定的原函数对于每一个频域的频率来说，其幅度和相位都是一定的。
幅度谱可以分为单边幅度谱以及双边幅度谱，单边幅值谱的每个频率所对应的幅值是该频率分量的模(即$A_n$)，双边幅度谱的每个频率的幅值是单边的一半（0除外），数值为$|F_n|$，但是双边的在$[-\infty,0]$也有函数图像，也就是说双边幅度谱的函数是一个关于y轴对称的函数。
单边相位谱每一个频率对应的数值为其相位，双边相位谱其中正半轴的图像与单边相位谱的一样，但是负半轴的图像与正半轴的图像刚好相反数，相当于以原点对称。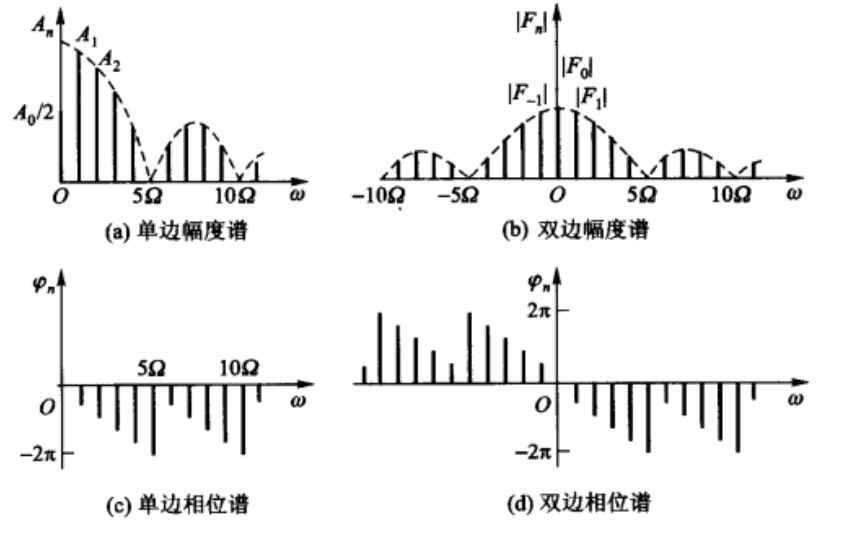

频率越大，频谱图的相邻间隔越小。
设f(t)傅里叶变换为F(w)，若时域为实偶信号——频域为实偶函数，若时域为实奇信号——频域为纯虚奇函数。相位谱的话，实偶信号相位谱未必恒为零。其对应的频域函数虽为实函数，但是若F（w）恒为正，那相位就是0. 若有正有负，那为负的时候，相位为±π

非周期信号的傅里叶变换

非周期信号的周期可以看作是无限大，其频谱的相邻谱线间隔$\Omega$趋近于无穷小，此时信号的频谱就是连续频谱，同时各频率分量的幅度也趋近于无穷小（仍保持一定比例关系）。因此引入频谱密度的概念：$F(j\omega)=lim_{T \to \infty}\frac{F_n}{1/T}=lim_{T \to \infty}F_n T$

关于傅里叶变换的过冲现象
实际上，我们使用傅里叶变换之后获得的函数在某些地方是“无限”也无法逼近的区域，拿合成方波的来举例，所用的频率越多，合成的波越接近方波，但是在棱角处却有着一定的突起，虽然在一直变小但是一直存在，这个就是过冲现象。像方波这种有突变的波形我们用连续的正弦波是无法完全拟合的，过冲现象随着频域的扩充只会减少但是不会消失，拉格朗日当年也是举了这个例子来反驳傅里叶的成果。
不过，拉格朗日是从数学的角度来看待的，但是傅里叶是个物理学家，他提出傅里叶变换就是为了使得在解析分析热过程时更加方便。从使用的角度来看经过傅里叶变换后的波形在能量上与原波形没什么差别（有也是目前测量精度无法计算的程度）。在实际工程使用时可以直接运用，