题目描述

在一个圆形操场的四周摆放 N 堆石子,现要将石子有次序地合并成一堆.规定每次只能选相邻的2堆合并成新的一堆，并将新的一堆的石子数，记为该次合并的得分。
试设计出一个算法,计算出将 N 堆石子合并成 1 堆的最小得分和最大得分。

输入格式 Input Format

• 数据的第 1 行是正整数 N，表示有 N 堆石子。
• 第 2 行有 N 个整数，第 i 个整数 a_i 表示第 i 堆石子的个数。

输出格式 Output Format

• 输出共 2 行，第 1 行为最小得分，第 2 行为最大得分。

输入：

4
4 5 9 4

输出：

43
54

---

想法

$O(n^3)$的暴力就不说了，写这道题主要是想记录一下四边形不等式优化。

四边形不等式优化

关于四边形不等式优化，大概是针对类似$f_{i,j}=min(f_{i,k}+f_{k+1,j}+C_{i,j})$或者$f_{i,j}=min(f_{i-1,k-1}+C_{k,j})$这种状态转移方程，其中的k可以用不等式缩小范围而不用一个一个枚举k，从而将复杂度降低.

第一个式子是石子合并的模型，第二个式子是求分段花费的模型。
首先是四边形不等式使用的条件，即$C_{i,j}$要首先满足四边形不等式条件以及单调性条件。

---

四边形不等式条件：

两个交错区间的$C_{i,j}$和，小于等于 小区间与大区间的$C_{i,j}$和

单调性条件：

小区间的$C_{i,j}$，小于等于 大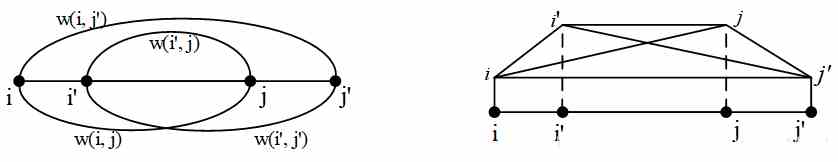区间的$C_{i,j}$。

---

只要满足这两个条件，就能使用四边形不等式优化。
不过一般也很难证明性质，可以考场上打表，要是和四边形不等式打出来的表一样就可以大概率认为它符合四边形不等式。

min和max的区别

min是指类似 $f_{i,j}=min(f_{i,k}+f_{k+1,j}+C_{i,j})$或者$f_{i,j}=min(f_{i-1,k-1}+C_{k,j})$的，max就是指 $f_{i,j}=max(f_{i,k}+f_{k+1,j}+C_{i,j})$或者$f_{i,j}=max(f_{i-1,k-1}+C_{k,j})$ 这种类型的状态转移方程。
假如把min改成max，呢么由于判断条件变了需要将使用的条件也变一下。
即求最大值时的条件为$C_{i,j'}+C_{i',j} \geq C_{i,j} +C_{i',j'}$ 这玩意叫反四边形不等式
还有 $C_{i',j} \geq C_{i,j'}$ 这是需要满足的新单调性：小区间的值大于等于大区间的值。

优化方法

用一个二维数组$s_{i,j}$记录一个区间最优决策点，如果$f_{i,j}$满足四边形不等式，呢么$s_{i,j-1} \leq s_{i,j} \leq s_{i+1,j}$

这个是石子合并的代码。

#include<bits/stdc++.h>
using namespace std;
long long n,a[20010],b[210][210],c[210],e[210][210],minn=10000000000ll,maxx=-1,smi[210][210];
int main()
{
    //freopen("a.in","r",stdin);
    //freopen("a.out","w",stdout);
    memset(b,10,sizeof(b));
    cin>>n;
    for(int i=1;i<=n;i++)cin>>a[i];
    for(int i=n+1;i<=n*2;i++)a[i]=a[i-n];
    n*=2;
    for(int i=1;i<=n;i++)b[i][i]=0,smi[i][i]=i,c[i]=c[i-1]+a[i];
    for(int i=1;i<=n/2;i++)
    {
        for(int j=1;j<=n;j++)
        {
            e[j][i+j]=max(e[j][j+i-1],e[j+1][j+i])+c[i+j]-c[j-1];
            /*注意这句，
              求最大值不能用四边形不等式，
              因为最大值不满足单调性，
              但最大值有一个性质，
              即总是在两个端点的最大者中取到。
            */
            for(int z=smi[j][i+j-1];z<=smi[j+1][i+j];z++)
                if(b[j][z]+b[z+1][i+j]+c[i+j]-c[j-1]<b[j][i+j])
                {
                    b[j][i+j]=b[j][z]+b[z+1][i+j]+c[i+j]-c[j-1];
                    smi[j][i+j]=z;
                }
        }
    }
    for(int i=1;i<=n;i++)minn=min(minn,b[i][i+n/2-1]);
    for(int i=1;i<=n;i++)maxx=max(maxx,e[i][i+n/2-1]);
    cout<<minn<<endl<<maxx<<endl;
    return 0;
}