电路分析基础学习笔记 一
本文最后更新于:2024年9月13日 早上
序言
记录了电路分析的学习,以总结为主复习时使用
其中大多数内容来源于丁老师的PPT,自学的时候帮助很大,
这里主要是整合划分以及总结一些自己觉得重要的点还有自己的理解
静态电路的分析就记在这里,动态电路的分析再开一页在这里!!
预备知识
一些基础的比较重要的但是没啥可说的都放到这里,想到啥写啥。
基础术语
1.二端元件two-terminal:
指有两个引出端子的元件,具有两个以上端子的元件称为多端元件,像晶体管就是一种三端元件,变压器是一种四端元件。在集总参数假设条件下,通常只关心元件端子上的特性(称为外部特性),而不注意其内部的情况。
2.拓扑图topologic graph:
指用一条线段来代表元件后得到的几何结构图。又称线图,简称图graph。这个电路图就可简化为图(b)的拓扑图。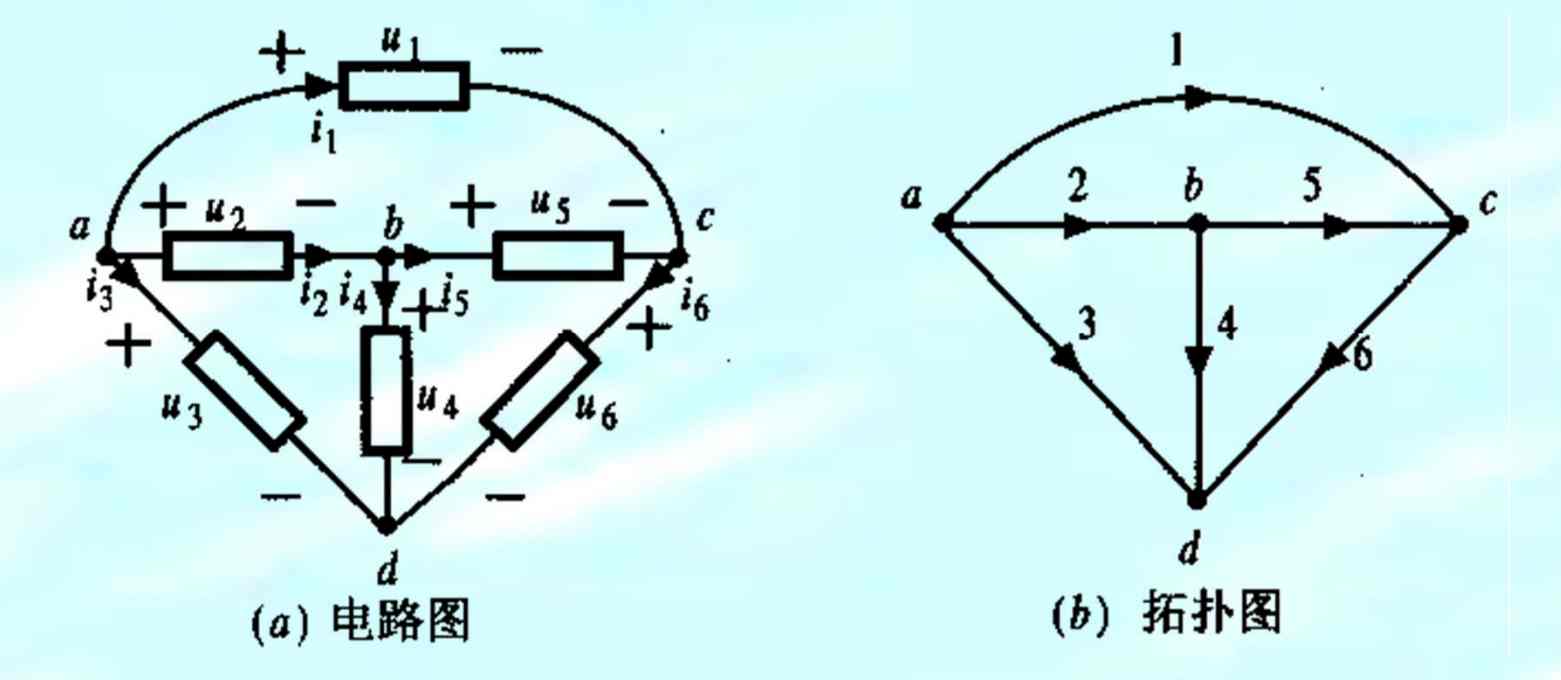
3.有向图directed graph:
指标明参考方向的图。通常图中的参考方向与相应电路图中电流(或电压)的参考方向相同。
4.支路branch:
电路图中的每一个元件,即图中的每一条线段,称为支路。有时为了方便,也可把某些元件的串联组合或并联组合当作一条支路来看待。在图论中也称支路为边。
5.节点node:
指支路的连接点。
6.路径path:
从某一节点出发,连续地经过一些支路和节点(只能各经过一次),到达另一节点,就构成路径。
7.回路loop:
如果路径的最后到达点就是出发点,这样的闭合路径称为回路。
8.网孔mesh:
在平面图中,构成回路的各支路围成一个区域。并且在区域内部不包含其它支路和节点的回路就称为网孔
9.电阻元件resistor:
分为 线性/非线性,时变/非时变等,本课程主要研究线性非时变电阻元件。
10.电压源:
理想电压源是指不管外部电路如何,其两端电压总能保持定值或一定的时间函数的电源。
11.电流源:
理想电流源是指不管外部电路如何,其输出电流(当方向与外电路电流相反时是吸收电功率)总能保持定值或一定的时间函数的电源。
12.受控源:
是指大小、方向受电路中其它地方的电压或电流控制的电源。即电压源的电压或电流源的电流不是给定的时间函数,而是受电路中某支路电压或电流控制。有源的二端口元件,分为受控电流源以及受控电压源。
无论是受控源还是电流源和电压源,都只用其输出/输入的性质,其本身的其余性质(电阻等)均忽略。(但是与回路中电流电压方向相反时实际上和电阻等效)
13.拓扑约束:
指组成电路的各个节点间电流及回路间电压的相互制约关系,这些关系仅由电路的结构(互连形式)决定,而与电路各支路中元件的电特性无关。该约束由基尔霍夫定律(KCL和KVL)体现。
14.元件约束:
来自元件自身的性质,即指每种元件对两个量(电压和电流)形成的一个约束。用VAR体现。
这两类约束是解决集总电路问题的基本依据。
15.网孔电流:
指设想在电路的每个网孔里沿着构成该网孔的各支路循环流动的假想电流
16.自电阻:
指各自网孔内所有电阻的总和。
17.互电阻:
指网孔与网孔之间的工有电阻。
18.互异性:
互易性是一类特殊的线性网络的重要性质。一个具有互易性的网络在输入端(激励)与输出端(响应)互换位置后,同一激励所产生的响应并不改变。
19.对偶性:
电路的对偶性体现在电路中的许多变量、元件、结构及定律都是成对出现,并且存在相类似的一一对应的特性。具有这样一一对应性质的一对元素(电路变量、 元件参数、 结构、 定律等),可称为对偶元素。
易知:如果电路中某一定理、公式或方程的表述是成立的,则将其中的元素用其相应对偶元素置换所得到的对偶表述也成立。
20.线性电路:
-指由线性元件、线性受控源及独立源组成的电路。若某线性电阻电路有唯一解,则该电路中任一支路电流和电压均可表示为电路中所有独立源的线性组合。体现为两个主要特性-齐次性和叠加性。
21.齐次性:
设网络的输入为f(t),输出为y(t),若 ,则:
22.叠加性:
设网络的输入为f(t),输出为y(t),若 ,则:
所以我们可得出这么一个结论:若且,呢么该系统就是线性系统。
23.网络函数:
线性、时不变电路在单一激励下,指定的响应(输出)与激励(输入)之比,称为网络函数,记为H,即
输入(激励)是独立电压源或独立电流源,输出(响应)是感兴趣的某个电压或电流。
24.数模转换器:
将输入的每一位二进制代码按其权的大小转换成相应的模拟量,然后将代表各位的模拟量相加,所得的总模拟量就与数字量成正比,这样便实现了从数字量到模拟量的转换。
这种电路的特点:
①从任一结点向左或向右看,其等效电阻均为;
②任一开关接UREF时到地的等效电阻均为,即流经该开关的电流为。
③电子开关受输入二进制代码的控制。
25.单口(one-port)网络:
在电路分析中可以把互连的一组元件看作为一个整体,从而和其他部分区分开,若这个整体只有两个端钮与外部电路相连接,则不管它的内部结构如何,我们统称它为二端网络或单口网络。二端网络中从一个端钮流进的电流必定等于另一端钮流出的电流,一个单口网络对电路其余部分的影响,决定于其端口电流电压关系(VAR)
26.输入电阻:
输入电阻等于将独立电源置零后,从端口看进去的等效电阻。“电源置零“的含义是:将电压源短路,使其输出电压为零;将电流源断路,使其输出电流为零。
电路等效
1. 等效定义: 两部分电路 B 与 C, 若对任意外电路 A,二者相互代换能使外电路 A 中有相同的电压、电流、功率,则称 B 电路与 C 电路是互为等效的.
2. 等效条件: B 与 C 电路具有相同的VAR 。
3. 等效对象: 任意外电路 A 中的电流、电压、功率。
4. 等效目的: 为简化电路方便分析(求解)
定理
欧姆定律(VAR)
在一个回路中,通过某段导体的电流和这段导体两端电压成正比,跟它的电阻却是成反比
中学阶段就已经很熟悉了,在此不做过多叙述欧姆定律解决的是元件上电压、电流的约束关系,这种约束取决于支路元件的性质,与电路结构无关;KCL和KVL阐述的是电路结构上电压、电流的约束关系,取决于电路的连接形式,与支路元件的性质无关。
基尔霍夫定律
节点电流定律(KCL)
任一瞬间,流向某一节点电流的代数和恒等于零。
直戳了当的结论,就是对于节点i,和它链接的电流为$I_i$,呢么可知 $\sum I_i =0$.及一个节点上流入的电流和流出的电流的代数和总为0.
所谓电荷守恒定律,即是说电荷既不能创造,也不能消灭。基于这条定律,对集总参数电路中某一支路的横截面来说,它“收支”是完全平衡的。即是说,流入横截面多少电荷即刻又从该横截面流出多少电荷,$\frac{dq}{dt}$在一条支路上应处处相等,这就是电流的连续性。那么对于集总参数电路中的节点,在任意时刻t, 它“收支”也是完全平衡的,因此KCL成立。
①KCL是电荷守恒和电流连续性原理在电路中任意节点处的反映;
②KCL是对节点处支路电流加的约束,与支路上接什么元件无关,与电路是线性还是非线性无关;
③ KCL方程是按电流参考方向列写的,与电流实际方向无关。首先要设出每一支路电流的参考方向,然后依据参考方向是流入或流出取号(流出者取正号,流入者取负号,或者反之)列写出KCL方程。
④ KCL具有普遍意义,它适用于任意时刻、任何激励源(直流、交流或其他任意变动激励源)情况下的一切集总参数电路。
节点电压定律(KVL)
对任何集总参数电路,在任意时刻,沿任意闭合路径巡行,各段电路电压的代数和恒等于零。 其数学表示式为 $\sum^{m}_{k=1} U_k(t)=0$ (沿任一回路) $U_k(t)$表示各个元件上的电压,m为回路中包含元件的个数。(代数和是指与回路绕行方向一致的支路电压取正号,相反的取负号。)
KVL的实质,反映了集总参数电路遵从能量守恒定律,或者说,它反映了保守场中做功与路径无关的物理本质。从电路中电压变量的定义容易理解KVL的正确性。如果自a点出发移动单位正电荷,沿着构成回路的各支路又“走”回到a点,相当求电压$u_{a-a}$, 显然应是$ V_a-V_a = 0$.
推论: 电路中任意两点间的电压等于两点间任一条路径经过的各元件电压的代数和。
KCL定律的推广应用主要应把握广义结点的正确识别;KVL定律的推广应用则要在充分理解电位单值性原理的基础上,正确列写式中各段电压的正、负。
特勒根定理
特勒根功率定理
任何时刻,一个具有n个结点和b条支路的集总电路,在支路电流和电压取关联参考方向下吸收的功率之和恒等于零
特勒根似功率定理
任何时刻,对于两个具有n个结点和b条支路的集总电路,当它们具有相同的有向图,但由内容不同的支路构成,在支路电流和电压取关联参考方向下,满足A电压和B电流乘积等于B电压和A电流乘积。
公式:$\sum U_A I_B=\sum U_B I_A$,满足U和I都是在有向图相同的支路上。该定理表明,在有向图相同的任意两个电路中,在任何瞬时t,任一电路的支路电压与另一电路相应的支路电流的乘积的代数和恒等于零。
①电路中的支路电压必须满足KVL;
②电路中的支路电流必须满足KCL;
③电路中的支路电压和支路电流必须满足关联参考方向(否则公式中加负号);
④定理的正确性与元件的特征全然无关。
互易定理
对一个仅含线性电阻的无源二端口电路$N_R$,其中一个端口加激励源,另一个端口作响应端口,在只有一个激励源的情况下,当激励与响应互换位置时,同一激励所产生的响应相同。
大概满足以下三种情况:
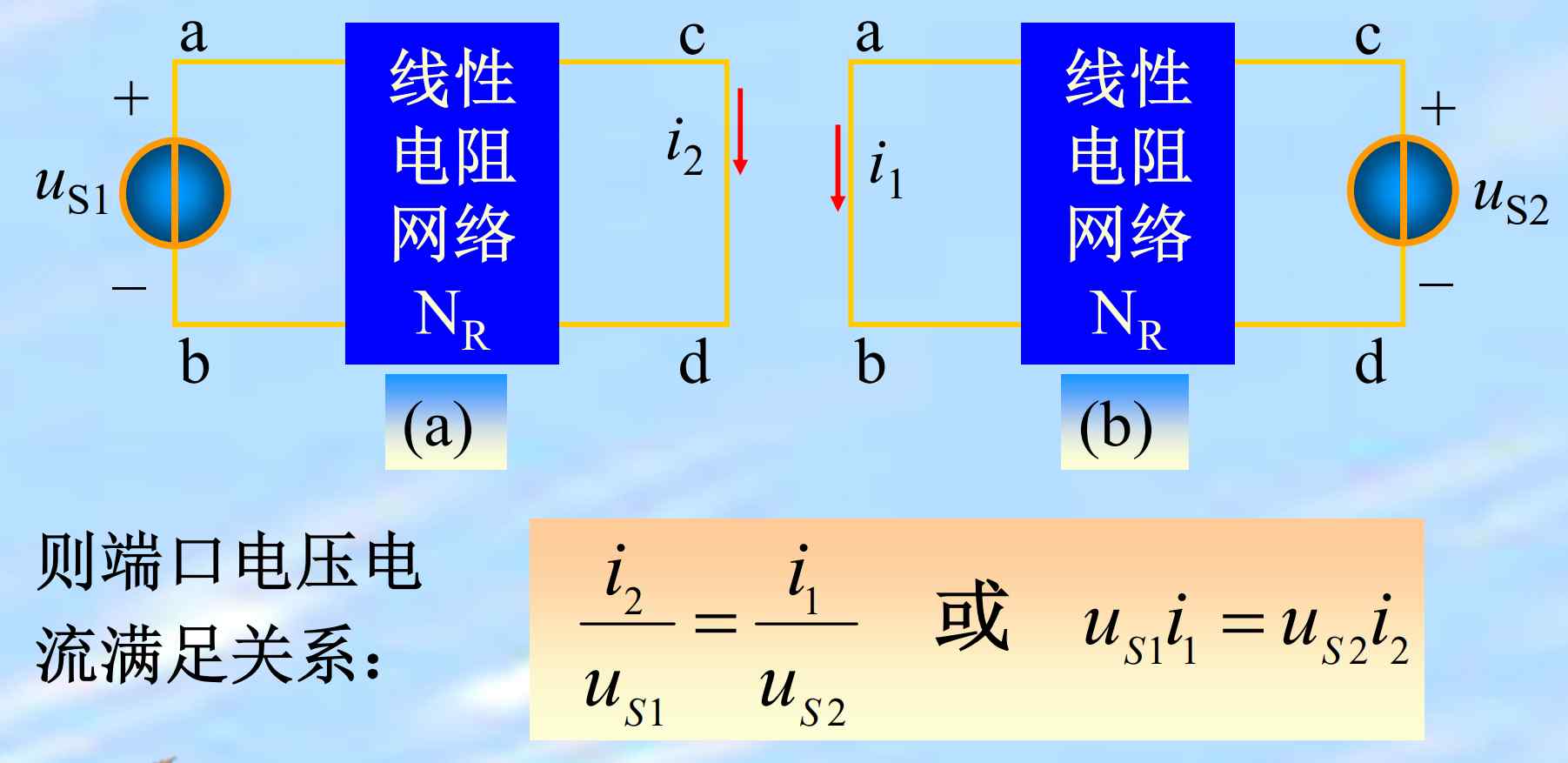
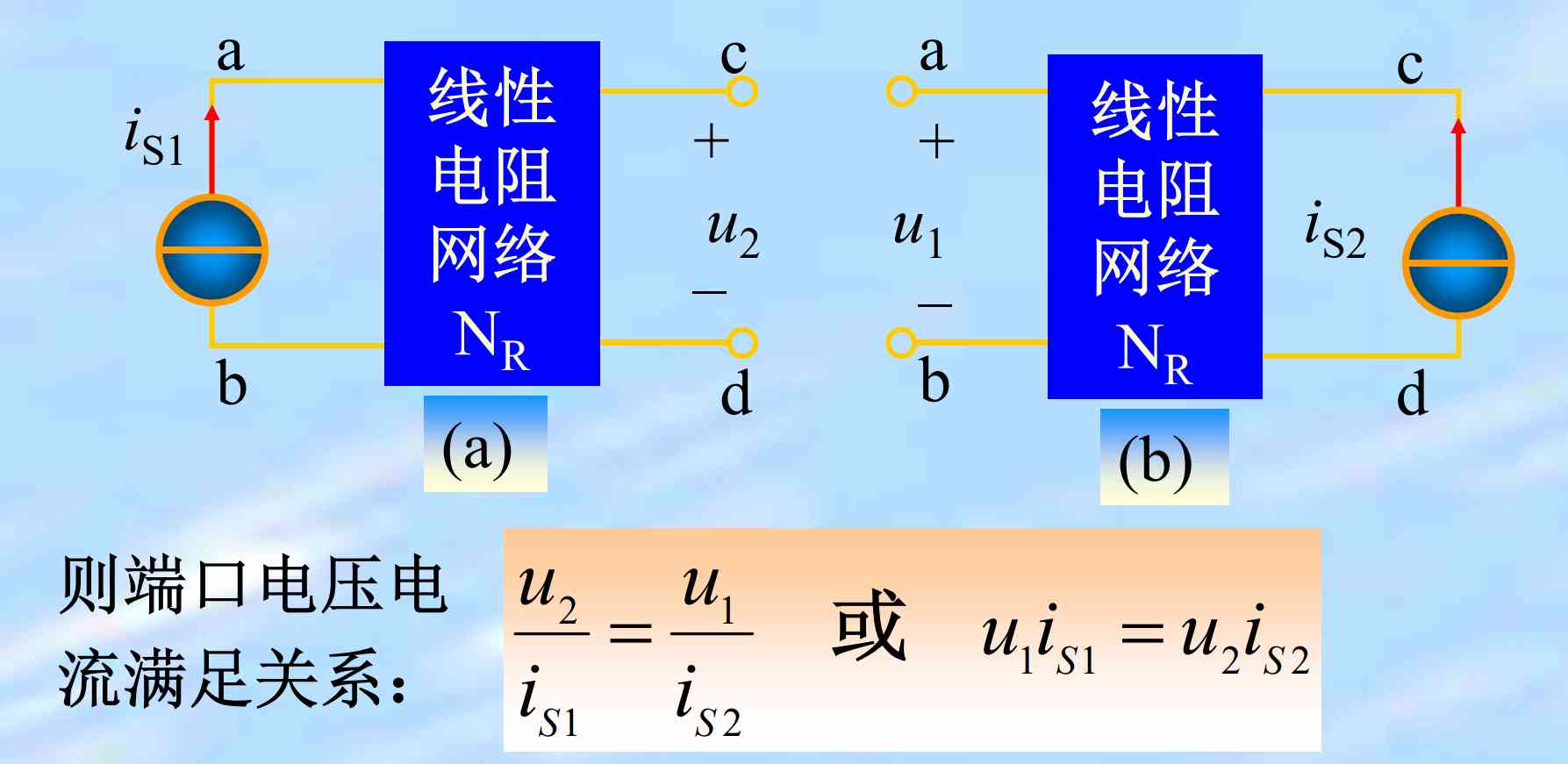
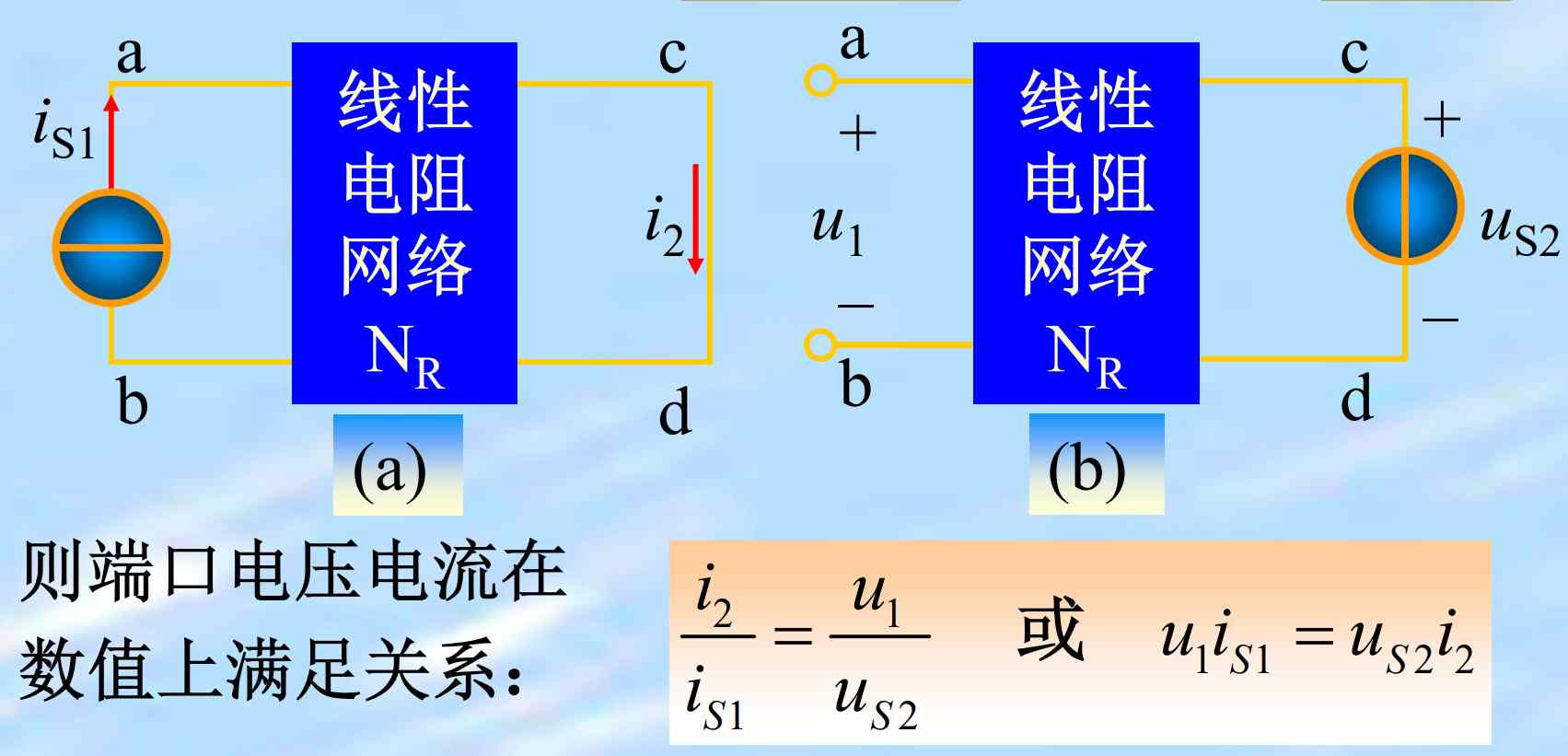
其实就是特勒根定律的特殊情况。
具有互易性的网络叫互易网络,互易定理是对电路的这种性质所进行的概括,它广泛的应用于网络的灵敏度分析和测量技术等方面。
① 互易前后应保持网络的拓扑结构不变,仅理想电源搬移;
②互易前后端口处的激励和响应的极性保持一致(要么都关联,要么都非关联);
③ 互易定理只适用于线性电阻网络在单一电源激励下,端口两个支路电压电流关系。
④含有受控源的网络,互易定理一般不成立。(update 2021/4/13需要受控源满足一定限制保证互易后相同)
叠加定理
齐次定理
当一个激励源(独立电压源或独立电流源)作用于线性电路,其任意支路的响应(电压或电流)与该激励源成正比。
齐次定理描述了线性电路的齐次性或比例性,若激励是电压源,响应是某支路电流i,则
置换定理 substitution theorem
具有唯一解的电路中,若知某支路k的电压为$u_k$,电流为$i_k$,且该支路与电路中其他支路无耦合,
则无论该支路是由什么元件组成的,都可用
(1) 电压等于$u_k$的理想电压源;
(2) 电流等于$i_k$的理想电流源;
(3) 阻值为$\frac{u_k}{i_k}$的电阻
这三种原件去置换.
① 替代定理既适用于线性电路,也适用于非线性电路。
② 替代后其余支路及参数不能改变。
③ 替代后电路必须有唯一解。
注意: “置换”与“等效变换”是两个不同的概念。
“替代”是用独立电压源或电流源替代已知电压或电流的支路,在替代前后,被替代支路以外电路的拓扑结构和元件参数不能改变,因为一旦改变,替代支路的电压和电流也将发生变化;而“等效变换”是两个具有相同端口伏安特性的电路之间的相互转换,与变换以外电路的拓扑结构和元件参数无关。
戴维南定理
含独立电源的线性电阻单口网络N,就端口特性而言,可以等效为一个电压源和电阻串联的单口网络。
起到的作用是简化电路,需要求出端口的VAR方程然后根据需要进行等效。
诺顿定理
含独立电源的线性电阻单口网络N,就端口特性而言,可以等效成一个电流源与电阻并联的网络
戴维南等效电路可等效变换为诺顿等效电路。所以只要求得Uoc、Isc、 R0中任意两个,则可得等效电路。本质上是相同的俩个东西。因为可以通过电路等效变化进行代换。
分析方法
2b方程法
指以支路电流和支路电压为变量列方程求解电路的方法。若电路有b条支路,则共有2b个变量。
KCL独立方程(n-1)个 && KVL独立方程(b-n+1个) && 支路方程(b个) 一共2b个
显而易见的是,2b法未知量较多,方程数目也很多,较为复杂,不建议使用。因此不在此详细说明。
支路电流法和支路电压法
支路电流/电压法实际上就是2b法消去部分方程的结果,因此相比于2b法更易计算。
支路方程法将2b方程法的方程组合表示电流集/电压集之间的关系,减少了联立方程的数目。
归纳、明确支路电流法分析电路的步骤。
第一步:设出各支路电流,标明参考方向。任取n-1个节点,依KCL列独立节点电流方程(n为电路节点数)。
第二步:选取独立回路(平面电路一般选网孔),并选定巡行方向,依KVL列写出所选独立回路电压方程。
第三步:如若电路中含有受控源,并且受控源的控制量就是某一支路电流,那么方程组中方程个数可以不增加,由列写出的基本方程稍加整理即可求解。如果受控源的控制量是另外的变量,那么需对含受控源电路先按前面讲述的步骤一、二去列写基本方程(列写的过程中把受控源先作为独立源一样看待),然后再加一个控制量用未知电流表示的辅助方程。
第四步:求解一、 二、 三步列写的联立方程组,就得到各支路电流。
第五步:如果需要,再根据元件约束关系等计算电路中任何处的电压、功率
网孔分析法
根据网孔电流以及回路关系构造网孔电流方程,第i个网孔的电流方程形式是$ (I_i \times \sum R_i) - \sum (I_j \times R_j)=U_i$,其中$I_i$是该网孔电流,$\sum R_i$是该网孔上所有电阻的和,$\sum (I_j \times R_j)$是与该网孔相交的其他网孔的网孔电流乘上相交部分的电阻的总和,$U_i$是该网孔上电压源输出的总和(带正负符号)。
节点分析法
通过与节点相连的电导以及节点的流出电流获得,实质上是节点的流入电流等于节点的流出电流。
形式是,其中是第j个节点的电位,是第i个节点和第个节点直接连的导线的电导。是第i个节点的流出电流。
很容易可以看出,这组成了一个线性方程组的形式,其中的系数矩阵由各个边上的电导组成。注意,当电导i=j时该值为该点链接的总电导(正),当i!=j时,电导值为负值。
电路分解方法
通过将电路划分为两个端口网络,将电路简化求解其VAR,然后联立两者的VAR方程求的其端口电压电流.
电路的等效变换
两个两端电路,端口具有相同的电压、电流关系,则称它们是等效的电路。
将具有相同VCR的电路替换原电路称为电路的等效变换,未变化的外电路A中的电压、电流和功率关系。(即对外等效,对内不等效)
单口网络等效电路
实际电压源、实际电流源两种模型可以进行等效变换,所谓的等效是指端口的电压、电流在转换过程中保持不变。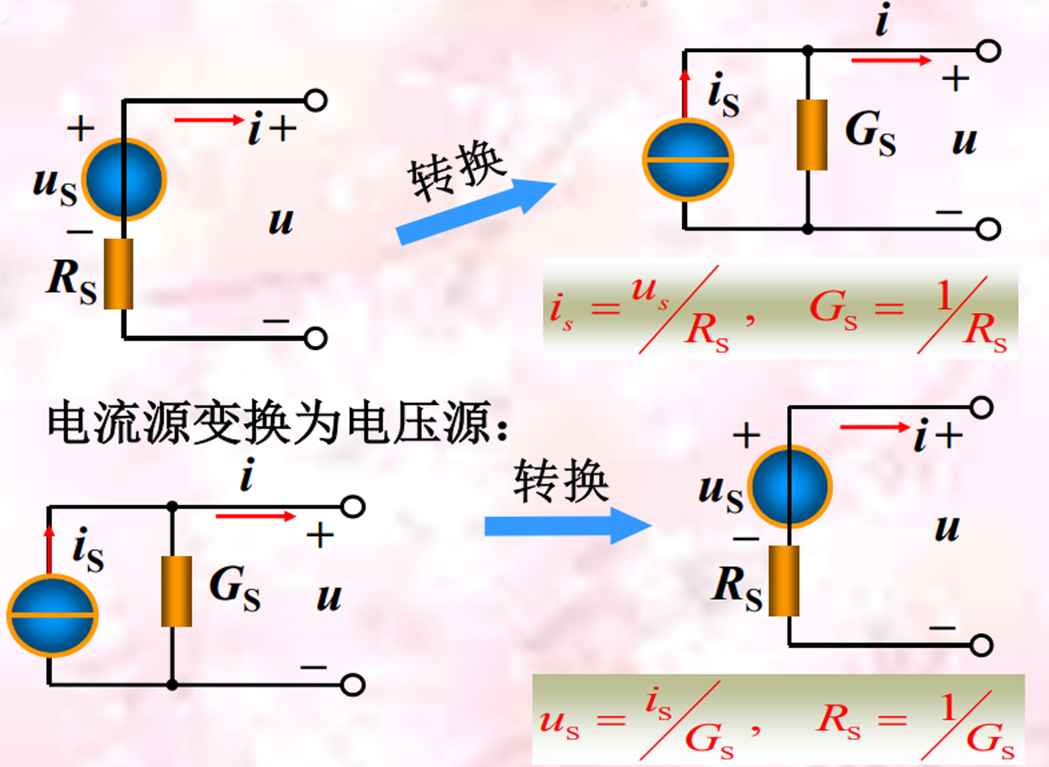
实际上是 电压源串联电阻 和 电流源并联电阻 这两个电路进行的转换,电阻值在变换中没有变化。新的电压源和电流源的输出值与原电流源和电压源的值和电阻构成欧姆定理
受控电流源的变换是受控电压源,反之亦然
实际上我们想要的是将复杂电路多个激励源转化为统一电压源用串联方式化简,或者同一电流源用并联方式化简,从而起到简化电路的作用。
T(Υ)形网络和∏(Δ)形网络的等效变换
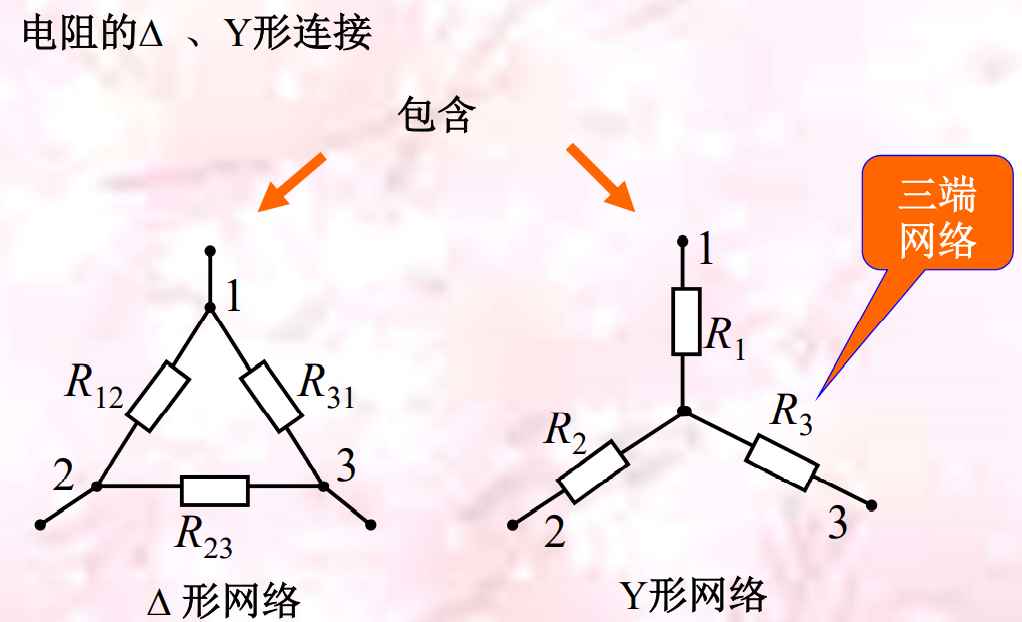
转化的具体推导很麻烦. . .这里就仅仅写下结论
三变Y电阻,Y变三电导。
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!