本来是在看费用流的题，结果发现EK+SPFA被卡了，然后发现了该方式的复杂度问题，便学习了Johnson使得DJ可以在负权图上运行。
DJ无法处理负权的边，一个显然的解决想法就是给所有的边都加上一个权值保证所有边非负，呢么算出最短路后就可以根据路径上边个数减去相应的增量。
这样想看起来很对，但是实际上是有漏洞的。比如这张图。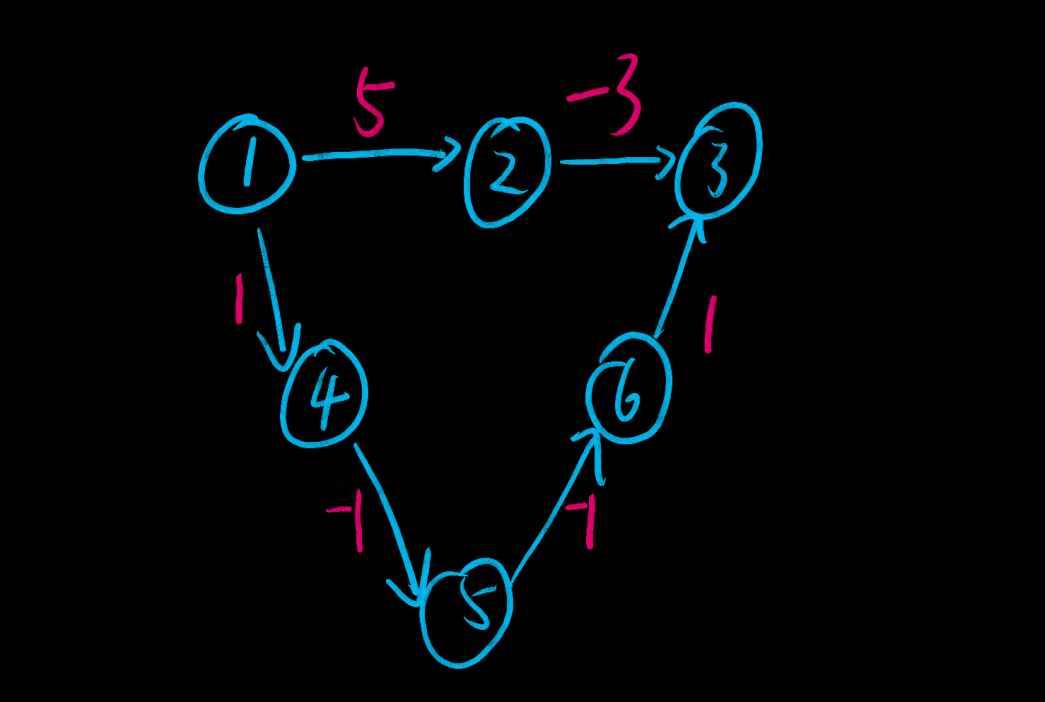

假如要求从1到3的最短路，原图最短路是[1-4-5-6-3]，但是加权至无负权边之后，[1-2-3]路径总会比原最短路短。
这就说明，单纯的同时加上同一个数是不行的。因此我们需要改变加权方式.
Johnson 算法则通过另外一种方法来给每条边重新标注边权。它为每一个点设置了一个势能$h_i$。对于一条从u到v，权值为$w_i$的边。将其边权设置成$W_i +h_u -h_v$。
势能$h_i$的获得则需要新建立一个和所有点连接的虚节点，与该节点相连的所有边边权为0，之后在该点上跑单源最短路，该点到点i的最短路就是点i的势能$h_i$。
输出时用pre数组记录下路径，减去势能即可。
证明源自OIerWiki。