高中时期关于网络流仅仅只是学习了EK求最大流，现进行重新学习并于此补充。

最大流问题

基础

最大流原理就是不停的寻找增广路，最后无流可走就是最大流，其中很妙的一点是增添了反向边这个东西，使得之前未走最优的路径可以通过反向边“反悔”，其他细节的部分源码中有注释。

Edmond_Karp
EK算法是在源点和汇点当中反复使用bfs寻找增广路，每找到一条可行路径就用数组记录下来并增加流量，复杂度就是O(nm^2)
源码

Dinic
Dinic是在EK的基础上进行了优化，用bfs找到增广路之后用dfs寻找所有路径并增加流量，添加了深度数组保证一次dfs可以找到多条可行路径，时间复杂度O(n^2m)，这里是源码。
这个是当前弧优化版本的Dinic，优化效果显著
实际中遇到的多是最大流问题的变种，需要良好的建模能力才能准确应用

---

最小割问题||顶点容量流

最大流最小割定理:网络的最大流等于最小割
这个等于是指在数值上的等于，具体证明不再赘述。最小割主要是分为割点和割边，割边就是明显的最大流问题，割点的话就需要对原图进行拆点转化
割点将一个点分为两个点，中间连上一条单向边，流量设为1.而原边的流量设置为极大数。显然，转变后两点之间流量为1的边才是有效边，而原边不会对流量产生干扰，如此将割点转换成割边的问题。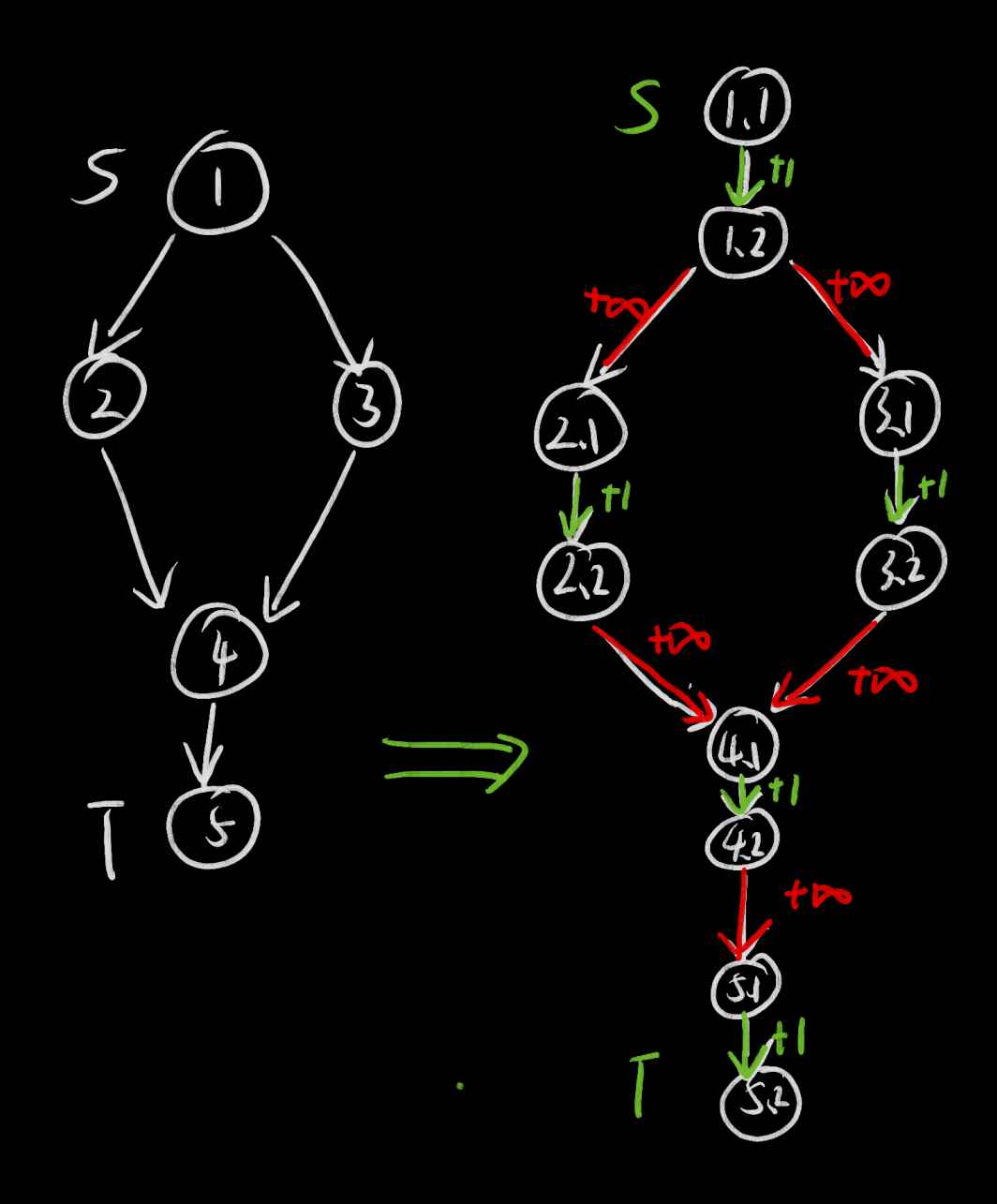

如图所示，在此时的图上跑最大流，红色边(原边)对答案起不到任何干扰，绿边(新创的边)才会制约答案。原理显然。
顶点容量流也和最小割点一样，使用拆点成边即可，不过此时新边为点的容量，原边容量不变

---

最大权闭合子图

闭合图：对于一个有向图G，存在点集合V，任取点u属于V，u的出边的另一个点也属于V，则为闭合图。
就是在闭合图内任取一起点，途径的点和终点必定都属于该闭合图。
最大权闭合子图：当每个点有一个权值w（有正有负），点权和最大的闭合图为最大权闭合子图。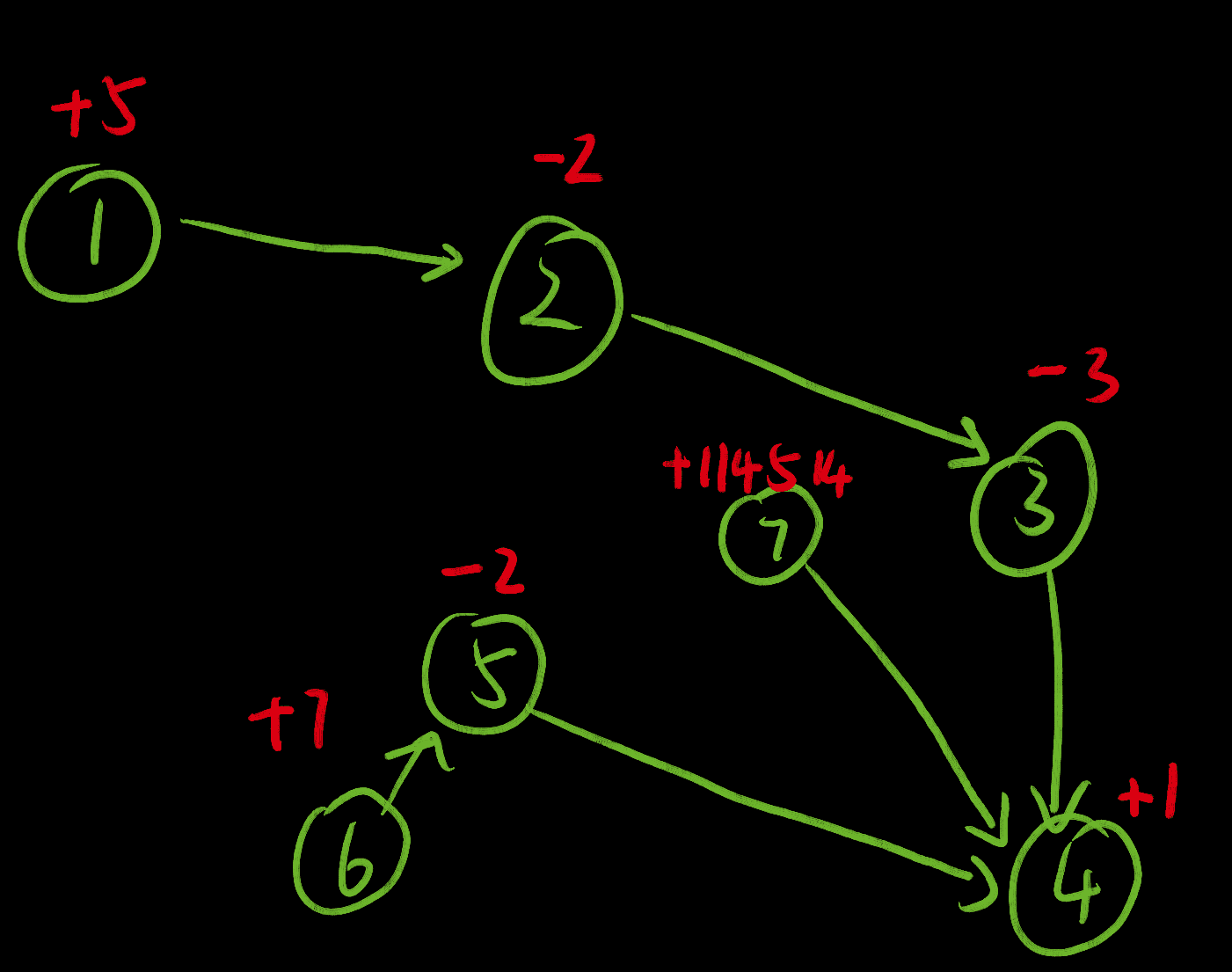

就像这张图片里的图，其中{1,2,3,4},{6,5,4},{7,4}为该图中的三个闭合图，而最大全闭合子图是{7,4}，权值为114514+1=114515.
这种题目也是通过最大流来解决，建立一个源点S和所有权值为正的点连边(源点→权值为正的点)，权值为该点的权值;再建立汇点E和所有权值为负的点连边(权值为负的点→汇点)，权值为该点的权值的绝对值。其他边的权值设为极大值。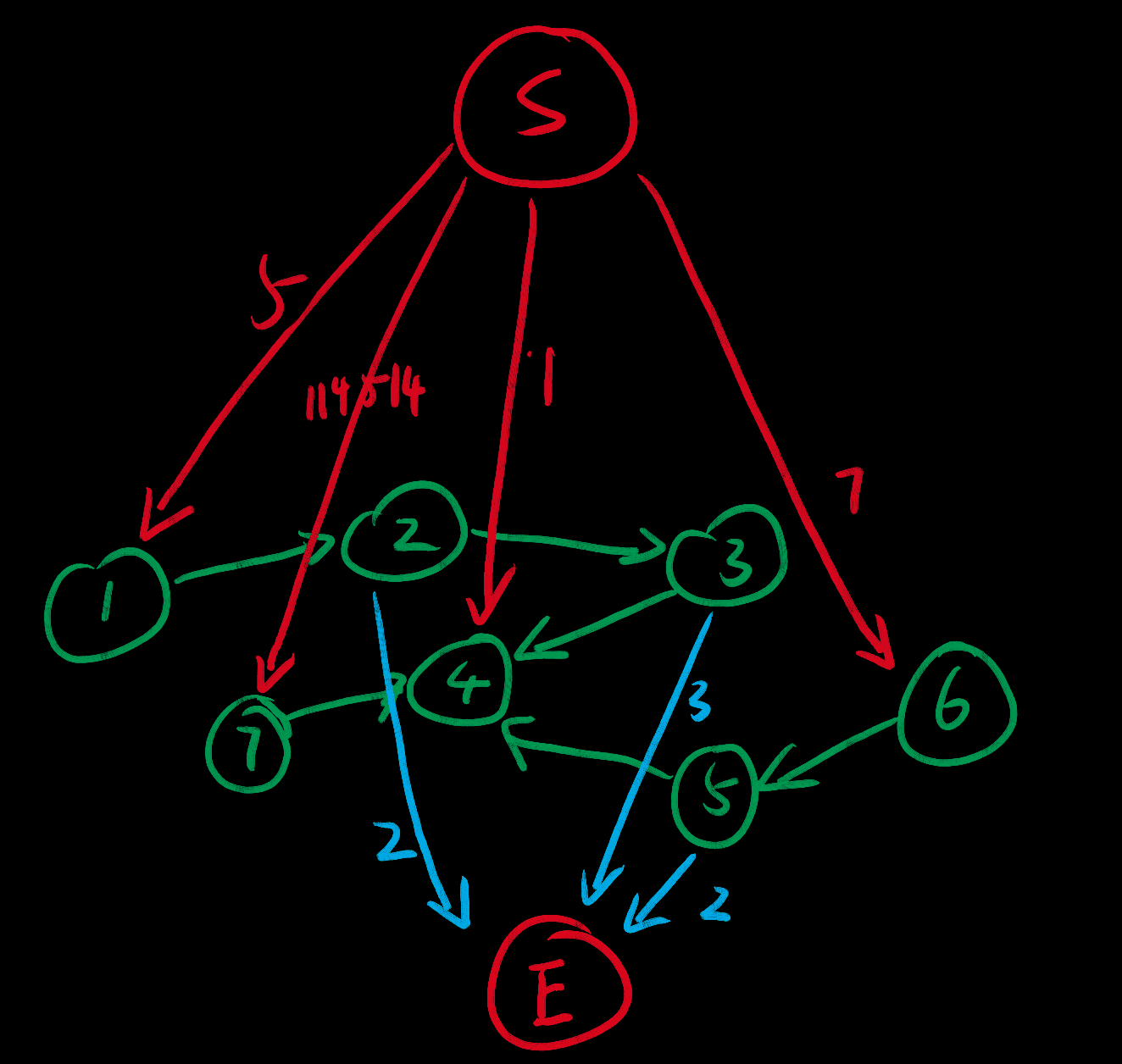

然后在新图上跑最大流，最终最大权闭合子图的值就是所有点权为正的权值之和-新图上的最大流
根据图片演示，应该很容易想到原理。
我们首先定义一个 “有效”的闭合子图为该图内所有点权之和大于0。由于闭合图的性质，我们可以得出所有有效的闭合子图就之和是我们所需的答案。
模拟一下网络流的过程，以一个节点开始必然会经过它之后的所有的节点，流向汇点E的部分就是所有有效的闭合子图的负权值之和。因为流向汇点的点均为负值节点。大于其边权的流量只能有该边权的流量通过;小于其边权的流量代表这个子图的总权值为负值，这个子图最终流向汇点的权值是其正值权值的总和，这部分权值不会计算在内，会在最后一步减去;而流向汇点的流量为0的边权则代表该点并不是有效的闭合子图的一部分。
因此得证 大权闭合子图的值 = 所有点权为正的权值之和 - 新图上的最大流

---

最小费用最大流

给定一个网络，每条边除了有容量限制，还有一个单位流量的费用。
当一条边的的流量为$f_i$ 时，需要花费$f_i \times Cost_i$的费用。则该网络中总花费最小的最大流称为 最小费用最大流.

SSP算法

SSP（Successive Shortest Path）是一个贪心的算法，每一次找到最短的可增广路进行增广，直到图上不存在增广路即可。
算法很简单，只要把EK或Dinic中的寻找增广路的部分换成SPFA即可，这里是EK替换后的源码。设网络最大流为f，呢么时间复杂度最坏情况为O(nmf)的

这并不是一个多项式时间复杂度，因为多项式时间复杂度要求算法花费的时间可以表示为一个关于输入数据规模$n$的多项式函数。 而在SSP算法中，最大流$f$并不一定能表示为关于$n$的多项式函数。假如构造$m=n^2 , f=2^{n/2}$的网络，该情况下 SSP 算法的时间复杂度将达到指数时间复杂度。

Primal-Dual 原始对偶算法

学习了Johnson算法后我们可以尝试使用DJ来代替SPFA进行最短路的查找。此时要解决的是势能设定问题，因为每跑一次费用流流量均会发生改变，相应的单位权值乘上流量变化量形成的权值增量也会改变。